"Le savant n'est pas l'homme qui fournit de vraies réponses ; c'est celui qui pose les vraies questions."1. Définition
Un polygone est une figure de la géométrie plane qui a plusieurs côtés. Le mot polygone est formé par poly (du grec polus) qui signifie plusieurs et gone (du grec gônia) qui signifie angle.
Exemple :
Un triangle est un polygone qui a trois côtés.
2. Classement des polygones
2.1. Polygone croisé
Un polygone est dit croisé s’il a au moins deux côtés sécants.
Exemple :
Cette figure est un polygone qui a 4 côtés. Deux de ses cotés sont sécants (c’est-à-dire se rencontrent en un point), alors il s’agit d’un polygone croisé.
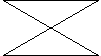
2.2. Polygone convexe
Un polygone est dit convexe s’il n’est pas croisé et si l’ensemble de ses diagonales se trouvent à l’intérieur du polygone.
Exemple : Un rectangle est un polygone convexe car premièrement il n’est pas croisé, et deuxièmement ses diagonales (en rouge) sont forcement à l’intérieur de la figure.
2.3. Un polygone non convexe
Un polygone non convexe est un polygone non croisé et qui a au moins une diagonale qui se trouve à l’extérieur de la figure.
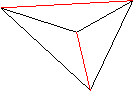
Exemple : Sur cette figure, on voit qu’une des diagonales (en rouge) se trouve à l’extérieur du polygone.
2.4. Un polygone régulier
Un polygone est dit régulier si ses côtés et ses angles sont égaux.
Exemple :
Un carré est un polygone régulier.
2.5. Un polygone isocèle
Un polygone est dit isocèle s’il possède au moins un axe miroir.
Exemple :
Un triangle isocèle est un polygone isocèle.
2.6. Un polygone rectangle
Un polygone est dit rectangle s’il possède au moins un angle droit.
Exemples :
Un carré, un triangle rectangle etc.
2.7. Un polygone équilatéral
Un polygone est dit équilatéral si ses côtés sont égaux.
2.8. Un polygone équiangle
Un polygone est dit équiangle si ses tous ses angles sont égaux.
2.9. Un polygone centrosymétrique
Un polygone est dit centrosymétrique s’il possède un centre de symétrie.
Exemple :
Un losange est un polygone centrosymétrique.
2.10. Un polygone rotocymétrique
Un polygone est dit rotocymétrique d’ordre n quand il présente un axe de rotation d’ordre n.
Exemple :
Un triangle équilatéral est un polygone 3-rotocymétrique (c’est-à-dire un polygone rotocymétrique d’ordre 3).
2.11. Un polygone scalène
Un polygone est dit scalène s’il ne possède pas un centre de symétrie.
3. Noms des polygones selon le nombre des côtés
Un polygone qui a trois côtés est appelé triangle ou trigone
Un polygone qui a quatre côtés est appelé quadrilatère ou tétragone.
Un polygone qui a cinq côtés est appelé pentagone.
Un polygone qui a six est appelé hexagone.
Un polygone qui a sept côtés est appelé heptagone.
Un polygone qui a huit côtés est appelé octogone.
Un polygone qui a neuf côtés nonagone ou ennéagone.
Un polygone qui a dix côtés est décagone.
Un polygone qui a 100 côtés est appelé hectogone.
Un polygone qui a 1000 côtés est appelé chiliogone ou chilogone.
Il faut noter qu’ici on n’a pas cité tous les noms des polygones. Pour lister l’ensemble des noms des polygones en fonctions de leurs côtés, il faut plusieurs jours d’écritures.
