"Le savant n'est pas l'homme qui fournit de vraies réponses ; c'est celui qui pose les vraies questions."Dans ce cours, on va étudier le cylindre de révolution.
1. Définition
Un cylindre de révolution appelé couramment cylindre, est une figure de la géométrie dans l’espace formée par deux bases circulaires parallèles et une surface latérale perpendiculaire aux deux bases.
Les deux disques circulaires constituent les bases du cylindre. La distance séparant les deux disques est appelée hauteur du cylindre.
2. Le patron d’un cylindre
Le schéma suivant constitue le patron d’un cylindre de rayon r et de hauteur h.
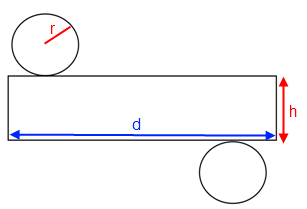
Les deux disques sont les bases du cylindre.
r : le rayon du cercle délimitant la base
h : la hauteur du cylindre
La distance d est égale à la circonférence du cercle de rayon r.
donc d= 2 x π x r.
3. Calcul de l’aire latéral du cylindre
En se référant du patron du cylindre (voir schéma patron du cylindre), l’aire latérale du cylindre est l’aire du rectangle de longueur d et de largeur h. Or on sait que d = 2 x π x r, alors :
Aire latérale = 2 x π x r x h.
4. Calcul du volume du cylindre
Le volume d’un cylindre est égal à l’aire de la base multiplié par la hauteur.
Aire de la base = π x r x r = π x r2
Alors Aire du cylindre = π x r2 x h
A = π x r2 x h
