"Le savant n'est pas l'homme qui fournit de vraies réponses ; c'est celui qui pose les vraies questions."1. Introduction
Un entier relatif est un nombre qui se présente comme un entier naturel mais qui porte un signe négatif (-) ou positif (+).
Ceux qui portent des signes négatifs sont appelés nombres entiers relatifs négatifs (ou entiers négatifs). Ceux qui portent des signes positifs sont appelés nombres entiers relatifs positifs (ou entiers positifs).
Exemple :
-1 est un nombre entier relatif négatif.
+200 est un nombre entier relatif positif.
Un nombre qui s’écrit avec un signe positif peut s’écrire sans signe.
Exemple :
+25 = 25. Au lieu d’écrire +25, on peut tout simplement écrire 25.
Remarque :
Tous les entiers naturels sont des entiers relatifs positifs.
L’ensemble des entiers relatifs est noté Z.
Alors Z= {… -3 ; -2 ; -1 ; 0 ; 1 ; 2 ; 3 ;…}
Les entiers positifs sont notés Z+ tandis que les entiers négatifs sont notés Z-.
Z+ = {0 ; 1 ; 2 ; 3 ;…}
Z-= {… -3 ; -2 ; -1 ; 0}
Ci-dessous, une droite représentant l’ensemble Z.
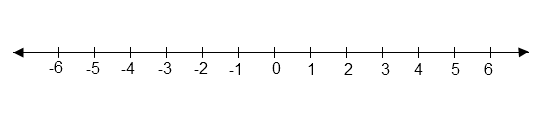
L’ensemble des entiers relatifs non nuls est noté Z*.
Remarque :
0 est un élément magique. Il est à la fois positif et négatif.
2. Calcul
Pour effectuer des opérations (addition, soustraction, multiplication, division etc.) avec des nombres entiers relatifs, il faut connaitre la table de multiplication et de division des signes.
– x – = +
– x += –
+ x += +
– / – = +
+ / + = +
+ / – = –
– / + = –
Exemples :
–2 x 4 = –8
(–2) x (–2) =+4=4
(+2) + (–2) = +2 – 2 = 0
(+2) / (–2) = – 1
(+8) / (+2) = +4 = 4
