"Le savant n'est pas l'homme qui fournit de vraies réponses ; c'est celui qui pose les vraies questions."
1. Définition
Un nombre décimal est un nombre qui peut s’écrire sous la forme 
.
P ∈ Z, k ∈N.
Exemples :
123, 453 est un nombre décimal car il est égal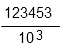 
.
-54,2 est un nombre décimal car il est égal à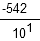 
.
76 est un nombre décimal car il est égale à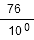 
.
Une autre définition d’un nombre décimal (la définition vue au primaire) dit qu’un nombre décimal est un nombre qui peut s’écrire avec une virgule.
Exemples :
453,973 est un nombre décimal car il possède une virgule.
12 est un nombre décimal car il est égal à 12,0.
L’ensemble des décimaux est noté D.
On note D= { }
La définition qui dit qu’un nombre décimal est un nombre qui possède une virgule est fausse. Elle n’est valable qu’aux enfants de la maternelle.
Remarque :
L’ensemble N et l’ensemble Z sont inclus dans D.
2. Les différentes parties d’un nombre décimal
Un nombre décimal est composé de deux parties :
La partie entière est la partie qui se trouve avant la virgule. La partie décimale est la partie qui se trouve après la virgule.
Exemple :
17,567 est composé de 17 qui est la partie entière et 567 qui est la partie décimale.
NB : Un nombre entier relatif est un nombre décimal dont sa partie décimale est nulle.
3. Calcul dans D (cas de présence des virgules)
Pour poser et effectuer des opérations (addition et soustraction) dans D, on pose les virgules sous les virgules.
Exemple :
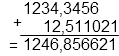
Pour la multiplication, on procède comme dans N. Après on compte le nombre des nombres après la virgule (Dans les différents facteurs) pour mettre la virgule dans le produit. Le nombre des nombres après la virgule dans les différents facteurs sera égal au nombre des nombres après la virgule dans le produit.
Exemple :
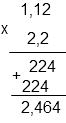
Dans 1,22, on a 2 chiffres après la virgule et dans 2,2, on a un seul chiffre après la virgule. Ce qui fait en tout 3 chiffres après la virgule.
On a ignoré les virgules lors de la multiplication, on a juste fait la multiplication de 122 et de 22. Et dans le résultat final, on a mis 3 chiffres après la virgule.
Pour la division, on éliminera les virgules en multipliant le dividende et le diviseur par le même nombre 10k, k est égale au grand nombre des nombres après la virgule entre le dividende et le diviseur.
Exemple :
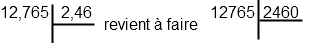
On a juste multiplié le dividende et le diviseur par 103 car le plus grand nombre des nombres après la virgule est 3.
4. Décomposition d’un nombre à virgule à une somme.
Exemple : 6473,564
6473,564 = 6473 + 0,564
Il faut noter qu’il y a plusieurs possibilités d’écrire cette égalité.
