"Le savant n'est pas l'homme qui fournit de vraies réponses ; c'est celui qui pose les vraies questions."1. Définition
Un nombre rationnel est un nombre qui peut s’écrire de la forme a/b, où a appartient à Z et b appartient à Z*. a est appelé numérateur et b dénominateur.
L’ensemble des nombres rationnels est noté Q.
Alors Q= {a/b| (a, b) ∈ Z x Z*}
Exemples :
1 est un nombre rationnel car il peut s’écrire sous la forme 1/1
1/5 est un nombre rationnel.
-263,5674 est un nombre rationnel car il peut s’écrire sous la forme -2635674/10000
NB : Un nombre qui n’est pas rationnel est irrationnel.
Attention!
Un nombre est rationnel si et seulement s'il admet une écriture décimale périodique ou finie.
Exemple:
1,4 est un nombre décimale fini alors 1,4 ∈ Q.
1,22222... est un nombre décimale infinie mais périodique (ici la période est 2), alors il ∈ Q.
1,34545... est un nombre décimale infinie mais périodique (ici la période est 45), alors il ∈ Q.
3,12231415... ce nombre décimale n'est ni périodique ni infinie. Alors il n'est pas rationnel. Donc il est irrationnel.
Remarque :
L’ensemble N, l’ensemble Z et l’ensemble D sont inclus dans Q.
Il y a une infinité de façon d’écrire un nombre rationnel.
Exemple :
2 = 2 /1 = 4/2 = 6/3 = 8/4 = 10 /5 etc.
2. Calcul dans Q
Soit a, b, c, d | (a, b) ∈ Z x Z* et (c, d) ∈ Z x Z*.
2.1. L’addition
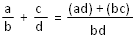
Exemple :
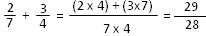
2.2. La soustraction
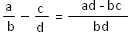
Exemple
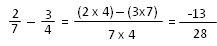
2.3. La multiplication
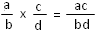
Exemple :
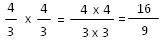
2.3. La division
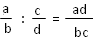
Exemple :
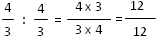
Une question ?
