"Le savant n'est pas l'homme qui fournit de vraies réponses ; c'est celui qui pose les vraies questions."1. Définition
Un nombre réel est un nombre qui peut représenter un point dans une droite graduée. Ceci dit qu’un nombre réel peut être représenté par une partie entière et une liste finie ou infinie de décimales.
L’ensemble des nombres réels est noté R.
L’ensemble des nombres positifs est noté R+.
L’ensemble des nombres réels positifs non nuls est noté R+*.
L’ensemble des nombres réels négatifs est noté R- .
L’ensemble des nombres réels négatifs non nuls est noté R-*.
Retenons :
L’ensemble des nombres entiers naturels, l’ensemble des nombres entiers relatifs, l’ensemble des nombres décimaux, l’ensemble des nombre rationnels et l’ensemble des nombres irrationnels sont inclus dans R.
2. Représentation graphique de l’ensemble R
On peut représenter l’ensemble R dans une droite graduée.
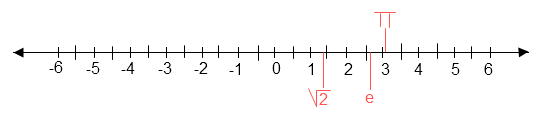
√2 = 1,4142...
π = 3,1415...
e= 2,718
3. Addition et multiplication
L’ensemble R muni des lois d’addition et de multiplication est un corps commutatif. Cela veut dire que :
