"Le savant n'est pas l'homme qui fournit de vraies réponses ; c'est celui qui pose les vraies questions."
Un triangle est une figure géométrique qui a trois côtés, trois sommets et trois angles.
La somme des angles d’un triangle est égale à 180o.
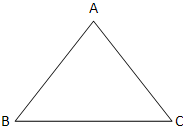
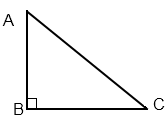
Ici on a le triangle ABC. A, B et C sont les sommets. [AB], [BC] et [CA] sont les côtes. Â,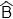 
et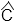 
sont les angles.
2.1. Un triangle en aiguille
Un triangle en aiguille (appelé aussi triangle dégénéré) est un triangle qui a au moins deux sommets confondus.
Un triangle en aiguille est un cas particulier dans la mesure où la somme de ses angles est nulle.
Exemple 1 :
Un point (.) est un triangle en aiguille dont tous ses trois sommets sont confondus. Ses angles sont nuls, ses côtés sont presque nuls.
Exemple 2 :
Ici le triangle ABC est un triangle en aiguille car les sommets B et C sont confondus. Les côtés [AB] et [AC] sont égaux. Le côté [BC] est presque nul. Tous ses angles sont nuls.
2.2. Un triangle plat
Un triangle est dit plat si tous ses sommets sont alignés. Il a donc deux angles nuls et un angle plat.
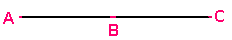
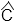 = = 0.
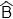= 180o.
2.3. Un triangle rectangle
Un triangle rectangle est un triangle qui a un angle droit. Le côté le plus long d’un triangle rectangle est appelé hypoténuse.
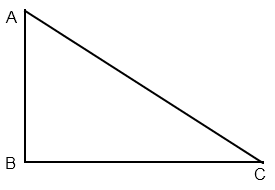
Le triangle ABC est un triangle rectangle en B.
AC est appelé hypoténuse.
Selon la loi de Pythagore : AC2 = AB2 + BC2
2.4. Triangle des arpenteurs
Le triangle des arpenteurs est un triangle rectangle qui a 5 comme hypoténuse. Les deux autres côtés mesurent respectivement 3 et 4.
2.5. Le triangle de l’écolier
Le triangle de l’écolier est un triangle rectangle dont les angles non droits mesurent 30o et 60o.
2.6. Le triangle de Kepler
Le triangle de Kepler est un triangle rectangle qui a un côté adjacent de longueur 1, l’hypoténuse et l’autre côté mesurent respectivement d2 et d.
2.7. Triangle isocèle
Un triangle est dit isocèle s’il a deux côtés égaux.
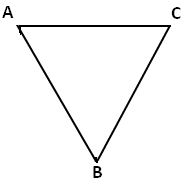
Le triangle ABC est un triangle isocèle car AB = BC.
2.8. Triangle iso-rectangle
Le demi-carré ou triangle iso-rectangle est un triangle qui est à la fois isocèle et rectangle.
ABC est un triangle iso-rectangle car AB = BC et 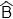= 90o.
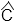 = = 45o.
2.9. Triangle iso-plat
Un triangle est dit iso-plat s’il est à la fois plat et isocèle.
Le côté le plus long est égal à la somme de deux autres côtés. Puisque les deux autres côtés sont égaux, alors le côté le plus long est égal à 2 fois l’un des autres côtés.
AB = BC.
AC= 2AB = 2BC.
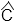 = = 0.
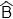= 180o.
2.10. Triangle équilatéral.
Un triangle équilatéral est un triangle qui a trois côtés égaux. Ses trois angles sont forcement égaux, alors chaque angle équivaut à 60o.
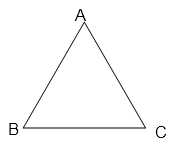
ABC est un triangle équilatéral car AB =BC = CA.
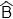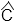 = = = 60o.
2.11. Triangle scalène
Un triangle est dit scalène s’il n’est pas plat et si ses trois côtés ont des longueurs différentes.
2.12. Triangle ambligone
Un triangle ambligone appelé aussi triangle obtusangle est un triangle qui a un angle obtus.
2.13. Triangle oxygone
Un triangle oxygone appelé aussi triangle actuangle est un triangle qui possède trois angles aigu.
2.14. Triangle d’or
Le triangle d’or est un triangle qui a deux angles de 72o et un angle de 36o.
3.1. Médianes
On appelle médiane d’un triangle (non plat), le segment qui a comme extrémités un sommet et le centre du côté opposé.
Les trois médianes d’un triangle se coupent en un point appelé centre de gravité. Ils divisent le triangle en six petits triangles de surface égale.
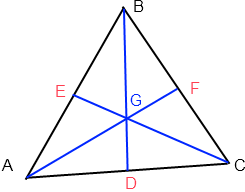
Ici on a le triangle ABC.
D, E et F sont respectivement les milieux de [CA], [AB], et [BC].
Alors BD, CE, et AF sont les médianes du triangle ABC.
G est le centre de gravité du triangle ABC.
Les petits triangles AEG, ADG, CDG, CFG, BEG et BFG ont la même surface.
3.2. Médiatrices d’un triangle
On appelle médiatrice d’un côté, une droite passant au milieu de ce côté et perpendiculaire à ce côté.
Les trois médiatrices d’un triangle se coupent en un point qui est le centre du cercle circonscrit à ce triangle.
d’, d’’ et d’’’ sont les médiatrices du triangle ABC. O, le point d’intersection des médiatrices est le centre du cercle circonscrit au triangle ABC.
3.3. Bissectrices
On appelle bissectrice d’un angle, la demi droite qui a pour origine le sommet de l’angle et qui partage l’angle en deux angles égaux.
Les trois bissectrices d’un triangle se coupent en un point qui est le centre du cercle inscrit au triangle.
Les demi-droites jaunes sont les bissectrices du triangle ABC. Le cercle jaune est le cercle inscrit au triangle ABC. Le point O est à la fois le point d’intersection des bissectrices et le centre du cercle jaune.
3.4. Les hauteurs d’un triangle
On appelle hauteur d’un triangle le segment qui part du sommet et qui est perpendiculaire au côté opposé. Le côté opposé est appelé base.
Les trois hauteurs d’un triangle se coupent en un point appelé orthocentre.
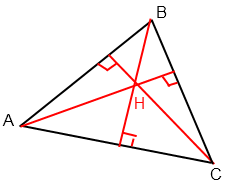
Les segments rouges sont les hauteurs du triangle ABC.
H est l’orthocentre.
Le périmètre d’un triangle est la somme des cotés qui forment le triangle.
Soit le triangle ABC suivant
P = AB + BC + CA.
P est le périmètre du triangle ABC.
Pour calculer la surface (aire) d’un triangle, on multiplie la hauteur par la base et on divise le produit par 2.
A = h x B /2
A : l’aire ou surface.
h : la hauteur.
B : la base.
