"Le savant n'est pas l'homme qui fournit de vraies réponses ; c'est celui qui pose les vraies questions."1. Définition
Un trapèze est un quadrilatère qui a deux côtés opposés parallèles.
Les côtés parallèles sont appelés bases.
ABCD est un quadrilatère.
AB est parallèle à DC (AB//DC).
Alors ABCD est un trapèze
2. Quelques trapèzes particuliers
2.1. Le parallélogramme
Tout parallélogramme est un trapèze particulier.
Exemples :
Le losange, le rectangle, le carré
2.2. Le trapèze rectangle
Un trapèze rectangle est un trapèze qui a au moins un angle droit.
Exemple 1 :
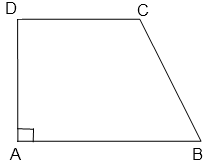
ABCD est un trapèze.
 = 90o
Alors ABCD est un trapèze rectangle en A.
Exemple 2 :
Un rectangle est un trapèze rectangle.
2.3. Le trapèze isocèle
Tout trapèze différent d’un parallélogramme est un trapèze isocèle s’il vérifie une des conditions suivantes :
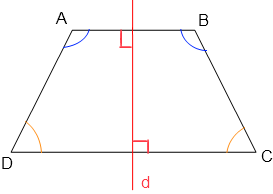
ABCD est un trapèze dont les bases sont AB et DC.
 = 
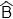alors ABCD est un trapèze isocèle.
= 
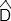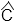alors ABCD est un trapèze isocèle.
AD = BC alors ABCD est un trapèze isocèle.
[AB] et [DC] on la même médiatrice d, alors ABCD est un trapèze isocèle.
3. Théorème du trapèze
Dans un trapèze, la droite joignant le point d'intersection des côtés non parallèles au point d'intersection des diagonales, passe par les milieux des côtés parallèles.
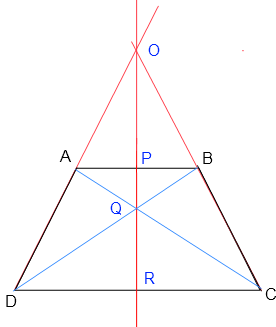
Les points O, P, Q et R sont alignés.
4. Calcul du périmètre
Le périmètre d’un trapèze est la somme des ses côtés.
Périmètre du trapèze ABCD = AB + BC + CD + DA.
5. Calcul de l’aire
La surface d’un trapèze est obtenue par la formule :
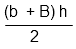
B et b sont les bases du trapèze.
h est la hauteur.
