1. Définition
Un cube est un prisme droit, un parallélépipède rectangle dont toutes les arêtes sont égales. Donc toutes les faces sont des carrés égaux.
2. Le patron d’un cube
Il y a 11 façons de présenter le patron d’un cube. Dans notre cas on va utiliser le développement en croix.

3. Calcul de la surface d’un cube
L’aire d’un cube est l’aire totale des 6 carrés formant le cube. Puisque les 6 carrés sont égaux, alors :
Aire = 6 (a x a)
Aire = 6a2.
A : aire ou surface
a : arête ou côté.
4. Calcul du volume d’un cube
Volume = arête x arête x arête
V = a x a x a
V = a3.
5. Calcul de la longueur de la diagonale
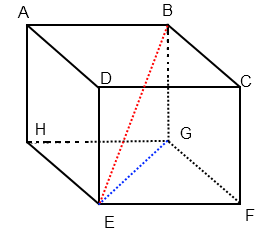
Ici dans notre schéma BE est une diagonale du cube ABCDEFGH. Et si nous observons bien le plan en trois dimensions, GBE est un triangle rectangle G. BE est donc l’hypoténuse.
Alors selon le théorème de Pythagore :
BE2 = BG2 + GE2.
On sait aussi que le triangle GHE est un triangle rectangle H. GE est donc l’hypoténuse. Selon Pythagore :
GE2 = HG2 + HE2
Maintenant remplaçons dans la première équation GE2 par sa valeur.
La première équation devient alors :
BE2 = BG2 + HG2 + HE2
Or on sait BG = HG = HE = a (a étant l’arête).
Alors BE2 = a2 + a2 + a2
BE2 = 3a2
BE = √ (3a2)
BE =a √ 3
Donc la diagonale est égale à a√ 3